क्लर्क ग्रेड II परीक्षा 23-10-2016 (RPSC) में पूछे गए प्रश्नों के सरल विस्तृत समाधान
Simple detailed solutions of Questions asked in Clerk Grade II (RPSC) LDC examination 23-10-2016
101. Let log1218= a, then log2416 is equal to
(1) (8 — 4a) /(5—a)
(2) (1/3)+a
(3) (4a-1)/(2+3a)
(4) (8-4a/(5+a)
1
Log1218=a
=log18 / log12 = a
=
log(9×2)/log(3×4)
={log(9) +
log(2)} / {log(3) + log(4)} Note: Value
of log(2) is 1
= log(3)2
+ 1 /
log(3) + log(2)2
= [2log(3) +
1] / [log(3) + 2log(2)]
= [2log(3) +
1] / [log(3) + 2] = a
Let log(3) =
x
2x+1 / x+2
=a
2x+1=xa+2a
2x-xa=2a-1
x(2-a)=2a-1
x=2a-1 /2-a
Or
log(3)=2a-1 /2-a
हमें ज्ञात करना है log
24(16) का मूल्य
Log (16) / log(24)
Log(2)4
/ log(8×3)
= 4log(2) /
[log(2)3 + log(3)]
= 4×1 /
3log(2) + log(3)
= 4 / [3 + log(3)]
, now put the value of log(3)
= 4/ [3 +
(2a-1 / 2-a )]
Let LCM 2-a
and solve
= 4(2-a) /
6-3a + 2a-1
= Answer
8-4a / 5-1
102. Let a, b, c and d be positive integers such that logab = 3/2 and logcd = 5/4.If a—c = 9, then b — d equals to
(1) 55
(2) 23
(3) 89
(4) 93
4
log a b=3/2 and log c d=5/4
b = a3/2 ,
d= c5/4
now to make it easy remove
denominators
let a1/2 = x and c1/4 =y
then b = x3 and d = y5, Note :
(b= a3/2 and x = a1/2 therefore x3= a3/2 or b= x3 similarly d=c5/4 and y = c1/4 therefore y5 = c5/4
or d= y5)
given a-c = 9
or x2 - y4 = 9
or (x-y2)(x+y2)=9
we have to find two factors
of 9 which are integers
now ; 9 can be expressed as
9x1 or 3x3
i.e. if we breach 9 as 3x3
then x-y2 = x+y2 which is not possible for any
existing integer
therefore x-y2 =
1 and x+y2 = 9
adding the two equations we
get 2x = 10 or x=5
and if x = 5 then y = 2 Note:
(Why : x+y2 = 9, 5+y2 = 9 , y2 =
9-5 , y2 = 4, y=2 )
therefore b = 125 and
d =32(Why: 5^3=125 and 2^4=32)
therefore b-d = 93 (Why: 125-32=93)
103. Successive discounts of p% and q% are equivalent to a discount of
(1) (p+q)%
(2) (p + q)/2 percent
(3) [(p+q-pq)/100] percent
(4) [p + q –(pq/100)] percent
4
P + (100-p)q /100
P + 100q-pq / 100
P + 100q/100 – pq/100
P + q - ( pq/100 )%
104. Let a2+b2=1; c2+d2=1 and ac+bd=O, then
(i) a2+C2 =1
(ii) b2+d2=1
(iii) ab + cd = O
Which one of the following is true ?
(1) Only (i) and (ii) are frue but (iii) is not.
(2) Only (iii) is true and (i) & (ii) are not true.
(3) All the three (i), (ii) and (iii) are true.
(4) All the three (i), (ii) and (iii) are false.
3
a2+b2=1, a2=1-b2, b2=1-a2
ac+bd=0, a=a and b=0 because a²+b2=1 similarly c=0 and d=1 because c2+d2 = 1
now examine options
(i) a2+C2 =1 (a=1 and c=0) 1+0= 1 is true
(ii) b2+d2=1 ( b=0 and d=1) 0+1 = 1 is true
(iii) ab + cd = O (a=1 b=0 so ab = 0, and c=0 and d=1 so cd = 0) is also true
105. The
salary of a person is increased by 20% of his original salary. But he received
the same amount even after increment. What is the percentage of his salary he
did not receive ?
किसी व्यक्ति
का वेतन उसके मूल वेतन का 20% बढ़ा है। लेकिन उन्हें
वृद्धि के बाद भी वही राशि मिली। उसे अपने
वेतन का कितना प्रतिशत प्राप्त नहीं हुआ?
12%
20%
50/3%
40/3%
3
Original salary Rs 100, Increased by 20%
new salary 120. He received Rs 100 out f 120. He did not received Rs 20*100/120
% or 2000/120 or 50/3%
106. A wire is cut into two pieces. The longer piece is 60% of the length of the wire. By how much percentage is the longer wire longer than the shorter piece?
एक तार दो टुकड़ों में काटा जाता है। लंबा टुकड़ा तार की लंबाई का 60% है। छोटे टुकड़े से लंबा तार कितना प्रतिशत लम्बा है?
(1) 20%
(2) 50%
(3) 120%
(4) None of these
2
Total wire
=100metre, Longer piece of wire =60% therefore shorter wire piece ia 100-60=40
metre. Longer wire is 60-40 =20 metre
longer than shorter wire or we can say 20*100/40 = 2000/40 = 50% longer
107. A certain sum of money generates a simple interest of 800 over 2 year period. The same sum of money invested at the same rate of interest on a compound interest basis for 2 years generates an interest of 900.
Find the principal.
एक निश्चित राशि 2 साल की अवधि में साधारण ब्याज से 800 उत्पन्न करती है। वही राशी 2 साल के लिए चक्रवृधि ब्याज पर, ब्याज की समान दर पर निवेश पर 900 का ब्याज उत्पन्न करता है। प्रिंसिपल खोजें (1) 1,200
(2) 1,600
(3) 2,000
(4) 2,400
2
माना कि मूलधन x है , दो साल में 800 ब्याज अतः एक साल में ब्याज 400.
दूसरे साल में मूलधन x+400 व उस पर ब्याज 900*400=500 या यों कहें 400 पर अतिरिक्त
ब्याज 100 अर्थात 100*100/400 = 25% अब 25 रूपये एक वर्ष का ब्याज है 100 रूपये पर
तो 50 रूपये दो वर्ष का ब्याज है 100 रूपये पर अतः 800 दो वर्ष का
ब्याज है 100*800/50 = 1600 रूपये पर
108. In a ∆ABC, AB = AC, P and Q are points on AC and AB respectively such that CB = BP = PQ = QA, then ∆AQP equals to
एक Δ एबीसी में, एबी = एसी, AC तथा AB पर क्रमशः P तथा Q बिंदु पर इस प्रकार है कि सीबी = बीपी = पीक्यू = क्यूए तो Δएक्यूपी बराबर है
(2) 5π/7
(2) 3π/4
(3) 2π/3
(4) 5π/6
1
Step 1
Draw a whole triangle ABC
Put P on side AC and Q on side AB
Join point B and P there will be a inner triangle BPC
In ∆BPC put angle P and C as b and angle c as b-a then b+b+b-a = π
3b= π+a
b = π+a/3
Step 2
Join point P on side AC with Q on side AB, there will be a inner triangle QBP
In ∆QBP put angle B and Q as a and angle P as π-(c+b)
Similarly there wiil also be a inner triangle APG
In ∆AG put angle A and P as C and angle Q as π-2c
Step 3
In ∆ QBP angle P = π-(c+b)
Π – 2a = π – (c+b)
2a = (c+b)
2a = c + (π+a)/3 (put value of b)
2a-(π+a/3)=c
6a-π-a)=3c
5a- π =3c
a= (π+3c)/5
Step 4
In ∆ APG
Π – 2c +a = π
a=2c
(π+3c)/5 = 2c
π+3c = 10c
7c=π
c=π/7
In AQP angel Q = π -2c put the value of c then
Angle Q = π – 2π/7
Angle Q = 7π-2π /7 or 5π/7
109. In a square ABCD, the sides AB, BC are produced to points P and Q respectively, such that BP = CQ. If AQ and DP intersect at E, then the angle PEQ is equal to
एक वर्ग एबीसीडी में, पक्ष एबी, बीसी क्रमशः पी और क्यू को इंगित करते हैं, बीपी = सीक्यू समान है। यदि एक्यू और डीपी ई पर टकराते हैं, तो कोण पीईक्यू बराबर है
(1) 3
/4
(2) 2π/3
(3) π/2
(4) 5π/12
3
Draw a square ABCD
Extend AB to P and BC to Q
Given BP = CQ therefore AP=BQ and DP=AQ
Since AQ intersects DP at E EP is perpendicular to AQ
Therefore in triangle PEQ angle E is 90 degree or π/2
110. The sum of the distances of the point (x, y) from the co-ordinate axes is
(1) √(x2+y2)
(2) x+y
(3) |x| + |y|
(4) √(x+y)
3
If x > 0 and y > 0 it will be xn + yn
If x < 0 and y < 0 it will be -xn + -yn
so in either case |x| + |y| will be the distance
111. The points (a, O), (O, b) and (1, 1) will be collinear if
(1) a+b+ab=0
(2) a+b=1
(3) 1/a + 1/b =1
(4) ab=1
3
Any two points on axis(x) and axis(y)will be collinear only in case sum of two is same in all cases, It is possible in case a+b=0 and the value of a and b is the same in all cases. 1/a + 1/b = 0 is the situation where it will be 0
Let A(a,0), B(0,b) and C(1,1) be the 3 collinear points
Let B divide the line segment joining AC in the ratio of k:1
Then, by section formula, the coordinates of B would be given by
(k+a/k+1 , k/k+1)
However, we already know that the coordinates of B is (0,b)
So, equating, 0 = k+a/k+1 i.e. k = -a
Also, b = k/k+1
Substituting k = -a, we get
b = -a/-a+1
i.e. 1/b = a-1/a
i.e. 1/b = 1-1/a
i.e. 1/a+1/b = 1
or
1/b+1/a=1
hence
1/a+1/b=1
hence
1/a+1/b=1
112. If a transversal line intersects three parallel straight lines, then the number of distinct values of the angles formed will be
(1) 2
(2) 4
(3) 6
(4) 12
1
transversal line intersects three parallel straight lines therefore it will make 6 angles but the value of 3 angles formed in one side will be same and value of 3 other angles formed in other side will be same. Therefore there will be only 2 distinct values
113. AB and CD are two perpendicular diameters of a circle of diameter d and centre at point O. What is the ratio of the area of circle to the area of triangle OAC ?
(1) ∏ :0.5
(2) ∏ :1
(3) ∏ :2
(4) ∏ :4
1
area of triangle OAC will be (r2/2)
(because radius is the same in both cases and sides of triangle are equal to radius of circle))
area of circle = ∏*r2
ratio of the area of circle to the area of triangle OAC
= ∏*r2 : r2/2
= ∏ : ½ or ∏ : 0.5
114. The sides of a right angled triangle are equal to three consecutive even numbers expressed in centimetres. What can be the area of such a triangle ?
(1) 12 cm²
(2) 24 cm²
(3) 48 cm²
(4) 100 cm²
2
side 1 = a, side 2 = a+2, side 3 = a+4
In a right angled triangle a2+(a+2)2 = (a+4)2
=a2+a2+4+4a = a2+8a +16
= a2+a2-a2-4a = 16-4
= a2-4a = 12
= a2-6a +2a -12 = 0
a(a-6)+2(a-6) a=2 or a=6
It can not tbe 2 as 22 +42 not equal to 62
therefore a=6 and a+2= 8
area of a right angled triangle = [a * (a+2)] /2
=(6*8)/2
=24 cm2
115. Three equal circles each of radius 'r' drawn on a plane in such a way that each circle touches the other two circles. A big circle is drawn in such a manner that it touches each of the small circles internally. Find the ratio between the radii of bigger circle to the smaller one.
(1) 2+√3 : 1
(2) 2+√3 : 2
(3) 2 : √3
(4) 2+√3 : √3
4
radius of small circles = r
difference in radius of big circle – radius of small small circles = x
radius of big circle r+x
Also r+x will be equal to r+ 2r/√3 , so x is equal to 2r/√3
Ratio between the radii of bigger circle to the smaller one
= r+ 2r/√3 : r
=√3r + 2r/√3 : r
=√3r + 2r : √3r
= √3 + 2 : √3
= 2 + √3 : √3
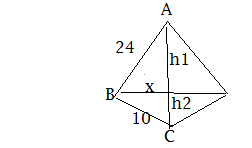
116. A right angled triangle ABC of sides AB = 24 m and BC = 10 m is rotated about its hypotenuse AC, then the ratio of volumes of bigger cone to the smaller cone is
(1) 13: 12
(2) 13:5
(3) 12:5
(4) 144: 25
4
If ∆ABC is rotated to its hypotenuse AC
AB=24 and BC =10 then AC is
242+102=√676 =262
therefore AC = h1+h2 = 26
x2+h12=242 = 576……(1)
x2+h22=102 = 100…….(2)
substracting (2) from (1)
h12 – h22 = 476
= (h1 – h2)( h1 + h2) = 476
=(h1 – h2) * 26 = 476
=h1 – h2 = 476/26 = 238/13
=h1 + h2 = 26
Add both
2h1 = 26+(238/13)
h1 = 13+(114/13)
h1 = (169+119)/13 = 288/13
Now h2 = 26-h1
h2 = 26-(288/13)
h2= (338-288)/13 = 50/13
ratio of volumes of bigger cone to the smaller cone is
288/13 : 50/13, =144:25
117. A ball of silver 4 cm in diameter is covered with gold. If the volume of the gold and silver are equal, then the thickness of gold is :
(1) 2 cm
(2) 1.038 cm
(3) 0.519 cm
(4) 0.5038 cm
3
Volume of ball of silver = 4∏r3 / 3
=4/3 * 22/7 * 23
= 704/21
If the volume of the gold and silver are equal then volume of gold plated ball is 704/13 + 704/13 = 1408/21
=4/3 * 22/7 * x3 =1408/21
=88 * x3 / 21 = 1408/21
=88x3 = 1408
=x3 = 16
x= 3√16 = 2.519
Gold plate = 2.519-2 = 0.519 cm
118. If sinA / sinB = p and cosA / cosB = q than tanB is equal to
(1) ± √[(q2+1)/(p2+1)]
(2) ± √[(p2+1)/(q2+1)]
(3) ± √[(1-p2)/(q2-1)]
(4) ± √[(q2-1)/(1-p2)]
4
sinA / sinB = p, cosA / cosB = q
sinA – p*sinB………………..(1)
sinB = sinA/p
similarly
cosA = q*cosB………………..(2)
cosB = cosA/q
We also know sin²A + cos²A =1, Sin²B+cos²B = 1
sin²A + cos²A = Sin²B+cos²B
substituting (1) and (2)
(p*sinB)²+(q*cos)² = p²sin²B+q²cos²B=1
p²sin²B - cos²B= -q² (cos²B+ Sin²B)
p²sin²B - Sin²B = (cos²B(1-q²)
sin²B(p²-1) = (cos²B(1-q²)
sin2B/cos2B = (1-q2)/p2-1
tan2B = (1-q2)/ (p2-1)
= ±√[(1-q2)/ (p2-1)] or = ±√[(q2-1)/ (1-p2)]
119. If a = cotA + tan A, b = cosecA — sinA, then (a2b)2/3 — (ab2)2/3 is equal to
(1) 10
(2) 1
(3) tan2A
(4) cot2A
2
cotA + tanA=a
We may easily solve the question by trigonometry ratios
Let A=45° then a=1+1, a2=4, b=(√2/1)-(1/√2)= 1/√2 , b2 = ½
Put these values in question
(a2b)2/3 — (ab2)2/3
[(4×(1/√2)]2/3 – [2×(1/2)] 2/3
(4/√2)2/3 – (1) 2/3
3√(4/√2)2 – 1
3√(16/2) – 1
3√8 – 1
2-1 = 1
Alternate method
a=1/sin.cos, b=cos2/sin2
[(1/sin2-cos2).(cos2/sin)]2/3 – [(1/sin.cos)-(cos4/sin2)]2/3
= (1/sin3)2/3 – (cos2/sin2)
=(1-cos2)/sin2
= sin2/sin2 = 1
120. If O < A < π/2 then consider the following :
I. √1- 2sinA/2 cosA/2 = cosA/2 — sinA/2
II. √1-2sinA/2 cosA/2 = sinA/2 - cosA/2
Which of the above is correct ?
(1) only 1
(2) only 11
(3) I and II both
(4) Neither I nor II
3
Assume A = 60°
Sin60/2 = sin30=1/2, cos30=√3/2
In case I
=√[1-(2*1/2)* (√3/2)] = √(3/2)— (1/2)
=√[1- (√3/2)] = (√3-1)/2
=√[(2-√3)/2)] = (√3-1)/2
Squiring both sides
=(2-√3)/2 = (4-2√3)/4
=(2-√3)/2 = 2(2-√3)/4
=(2-√3)/2 = (2-√3)/2
In case II
=√[1-(2*1/2)* (√3/2)] = (1/2)-√(3/2)
=√[1- (√3/2)] = (1-√3/)/2
=√[(2-√3)/2)] = (1-√3/)/2
Squiring both sides
=(2-√3)/2 = (1+3-2√3)/4
=(2-√3)/2 = 4-(2-√3)/4
=(2-√3)/2 = 2(2-√3)/4
=(2-√3)/2 = (2-√3)/2
Both I and II are correct
121. The mean and median of a frequency distribution be 55.60 and 52.40. What is the mode of the distribution ?
(1) 42
(2) 44
(3) 46
(4) 48
3
Mode= 3Median-2Mean
Mode= 3*52.40 – 2*55.60
Mode= 157.20-111.20=46.00
122. If x and y are related as 4x + 3y = 11 and mean deviation of x is 5.40. What is the mean deviation of y ?
(1) 7.2
(2) -7.2
(3) 3.8
(4) —3.8
1
X=11/4-3y/4 and y=11/3-4x/3
Mean deviation of x = 5.40, or 11/4-3y/4=5.40
Therefore deviation of mean of y = 5.40*(11/3-4x/3)/(11/4-3y/4)
=(5.40*4)/3 = 7.20
123.If the mean of A and B is 30, the mean of C and D is 20, then which of the following is/are correct ?
I. The mean of B and C must be greater than 25.
II. The mean of A and D must be less than 25.
Select the correct answer using the code given below :
(1) I only
(2) II only
(3) Either I or II
(4) Nither I or II
4
Mean of A and B =30, A+B/2=30, (20+40)/2 = 30, A=20 and B=40 or A=40 and B=10
Mean of C and D =20, C+D/2=20, (30+10)/2 = 20, C=30 and D=10 or C=10 and D=30
Mean of B and C = (40+30)/2 = 35 or (20+10)/2 = 15. It is not correct that mean of B and C must be greater than 25
Mean of A and D = (20+10)/2 = 15 or (40+30)/2 = 35. It is also not corret that mean of A and D must be less than 25
124. The missing frequency from the following data, given that the median mark is 23 is :
Mark 0-10, 10-20, 20-30, 30-40, 40-50
Students 5, 8, 10, ?, 7, 3
(1) 4
(2) 6
(3) 8
(4) 10
2
Let the missing frequency =x
Convert into cumulative frequency 5, 13, 23, 23+x, 26+x
Median =L1+ {[(n/2)-cf]/f} * i
Since median mark is 23 the median group is 20-30
20 is L1 and Median is 23 i.e 20+3
Median =L1+3
So value of {[(n/2)-cf]/f} * I is 3
Putting values n=26+x, cf=13, f=10 and i=10
3=[{(26+x)/2)/10]-13}*10
3=(26+x-26)/2
=26+x-26=6
=x=6
125. If the mean of a, b, c is Ml and a2, b2, c2 is M2, then one mean of ab, bc, ca is
(1) (Ml2 - 3M2) /3
(2) (3Ml2 - M2) /3
(3) (3Ml2 - M2) /2
(4) (3Ml2 - 3M2) /2
3
(a+b+c)/3 = M1, a+b+c=3M1
(a+b+c)2 = 3M12
9M12 =a2+b2+c2 +2(ab+bc+ca)......(1)
3M2 =a2+b2+c2……..(2)
Subtracting 2 from 1
9M12-3M2 = 2(ab+bc+ca)
(9M12-3M2)/2 = ab+bc+ca
Mean of ab+bc+ca = [(9M12-3M2)/2]/3
Mean of ab+bc+ca = (3M12-M2)/2
126. Study the following pie chart and answer the question number 126-127 :
A = Paper =126°
B = Advertisement 54°
C = Binding 45°
D = Printing 90°
E = Royalty 36°
F = Miscellaneous 9°
Expenditure incurred in bringing out a book by publisher.
Question: If there is a 10% change in existing expenditure on paper, then what will be the new expenditure on paper against total expenditure ?
(1) 31.66% or 38.5%
(2) 31.66% or 38.3%
(3) 31.5% or 38.5%
(4) 31.5% or 38.3%
3
There is 10% change in expenditure on paper then expenditure on paper may be 126+10% of 126 = 133.6*100/360 = 38.5%
or 126-10 of 126 =113*100/360 = 31.5%
127. If 12000 copies are published and miscellaneous expenditure on them amount to 14,625 and the publisher earns a profit of 20%, then marked price of each copy is :
(1) ₹ 48.75
(2) ₹ 58.50
(3) ₹ 48.25
(4) ₹ 58.75
2
Misc expenses 14625 on 12000 copies or 1.22 on one copy
Misc expenses are 9 out of 360 or 1.22 is equal to 9 then 360 is equal to 1.22*360/9 = 48.80
Cost price per copy 48.80 add profit 20% in 48.80*120/100 = 58.50
128. The angles of depression and elevation of the top of a wall 24 m high from top and bottom of a tree are respectively 60° and 30°. The ratio between the height of tree to its distance from the wall is
(1) 4:√3
(2) 2√3:1
(3) √3:4
(4) 1:2√3
1
In ∆ABC BC = 24√3
In ∆DAC ∠A =60º
DE/AE = x/24√3 = √3
x= √3 * 24 * √3
x = 3*24 = 72
height of tree = 72+24=96
ratio 96: 24 * √3 or 4:√3
129. In the adjoining figure, if BD || RS || PQ, CP = PD = 11 cm, AR = RD = 3 cm, BD = x, RS = y, PQ = z, then the ratio of values of y and z are :
(1) 6:11
(2) 3:11
(3) 1:2
(4) 1:1
4
∠A is common AR/AD = 3/3
∠ARS is congruent to ∠ADB
RS/DB = AR/AD and RS/x = 3/6 = ½ = y/x
Similarly Q/x = 11/22 =1/2 = z/x
Therefore the ratio of values of y and z are 1:1
130. Number of real factors of the polynomial x4 + 4x3 + 3x2 — 2x — 6 is :
(1) 4
(2) 2
(3) 3
(4) None of these
2
Factorize x4 + 4x3 + 3x2 — 2x —6
(x2 + 2x +2) (x+3) (x-1) = 0
Apply quadric formula for (x2 + 2x +2)
X=(-b ± √b2 – 4ac)/2a
Here a=1, b=2 and c=2
Accordingly x= -2 +√22 -4*1*2 or x= (-2+√ -4)]2 and x = (-2 - √ -4)]2
Since both these are not a real factor there are only 2 factors x= -3 and x = 1
131. The -integer number whose cube is the integer 912673, is :
(1) 107
(2) 87
(3) 97
(4) None of these
3
912673 = 912(9) 613(7) = 97
132. The median of first 10 prime numbers is:
(1) 11
(2) 13
(3) 12
(4) 14
3
2,3,5,7,11,13,17,19,23
(11+13)/2 = 12
133. If tanθ + secθ = x and 0< θ < π/2 then tanθ = ?
(1) (x2—1) /2x
(2) (x2+1) /2x
(3) (x2—1) /x
(4) (x2—1) /x
1
x= tanθ + secθ
Sec2=x-tan2
sec2 = x2 – 2x*tan + tan2
sec2 – tan2 = x2 – 2x*tan
x2-2x*tan – 1 = 0
2x*tan = x2 – 1
Tan =( x2 – 1 )/ 2x
134. If cos2A+cosA= 1, then sin4A+sin2A=
(1) -1
(2) 1
(3) 0
(4) 2
2
cos2A+cosA= 1
cos2A + cosA = 1
cos2A+ 1 – sin = 1
(1-sin2A) + 1 – sin = 1
1+sin2A – 2sin + 1-sin = 1
Sin2A – 2sin – sin = 1-1-1
Sin2A - sin = -1
Squire both sides
Sin4A + sin2A = 1
135. If an equilateral triangle is inscribed in a circle of area 48 π square units, then the perimeter of the triangle is :
(1) 72 units
(2) 48√3 units
(3) 36 units
(4) 48 units
3
Area of circle = 48 π square units
Radius of circle = √48 π
1 side of inscribed equilateral triange = 2 √[r2-(r2/2)2]
=2√[r2-(r2/4)]
=2√[48-(48/4)
=2√[48-12)
=2√[36) or 2*6 = 12
One side = 12 then perimeter of triangle is 12*3 = 36 units
136. If centroid of a triangle formed by the points (a, b), (b, c) and (c, a) is at the origin, then the mean of a3, b3, c3 is equal to
(1) a +b+c
(2) abc
(3) 0
(4) 3abc
2
Formula to find centroid in co-ordinate geometry is
(x,y) = (x1+x2+x3)/3 , (y1+y2+y3)/3
Then centroid of given triangle is [(a+b+c)/3 , (a+b+c)/3]
Since it give at the origin a+b+c = 0
Now recall the identity
a3+b3+c3–3abc =(a+b+c)(a2+b2+c2 – ab-bc-ca)
since a+b+c = 0 it gives a3+b3+c3=3abc
mean of 3abc = 3abc/3 = abc
137. A sum of money at compound interest doubles itself in 5 years. It will amount to eight times itself in :
(1) 20 years
(2) 12 years
(3) 15 years
(4) 10 years
3
Principal (p) becomes 2p in 5 years, it will beome 4p in 10 years and 8p in 15 years
138. X, Y and Z start a business. X invests 3 times as much as Y invests and Y invests two-third of what Z invests.
The ratio of capitals of X, Y and Z is :
(1) 3: 9: 2
(2) 6: 2: 3
(3) 5: 3: 2
(4) 6: 10: 15
2
Z=a, y= 2a/3, x= 2a*3/3 or 6a/3
6a/3 : 2a/3 : a/1
(6a : 2a : 3a)/3
6:2:3
139. The ratio of the son's age to the father's age is 1 : 4. The product of their ages is 196. The ratio of their ages after 5 years will be :
(1) 1:3
(2) 3:10
(3) 4:11
(4) 14:5
3
Now son age = x years then father age = 4x product x*4x = 196
4x2 = 196, x2 = 49, x=7
Son = 7 year father = 28 year
After 5 years
Son = 7+5=12 and father = 28+5 = 33
Ratio = 12: 33 or 4:11
140. A man spends 80% of his income. His income is increased by 20% and he increases his expenditure by 10%. His savings are increased by :
(1) 30%
(2) 20%
(3) 32%
(4) 60%
4
Income 100 – expenditure 80 = saving 20
Income 100+20 – expenditure 100-12 = savings 120-88 = 32
Savings increased 32-20=12 over 20
Therefore percentage increase 12*100/20 = 60%
141. The polynomial which when divided by (x2 + x + 1) gives quotient (x — 2) and remainder 3, is :
(1) x3—x2-X+ 1
(2) x3—x2—x+1
(3) x3—2x2+X+ 1
(4) x3—x2—x—1
1
(x2+x+1)(x-2) + 3
(x3+x2+1)-2x2-2x-2+3
=x3-x2-x+1
142. When the price of a motorcycle was increased by 15%, its sell fell down by 15%. The effect on money receipt was :
(1) 15% decreases
(2) 2.25% decreases
(3) 7.5% increases
(4) no effect
2
Price =100 increase to 115
Sale decrease to 85
Total money receips earlier 100*100 = 10000
Total money receips now 115*85 = 9775
Total receipts fall 10000-9775 = 225 on 100
Effect on money receips 2.25*100/10000 = 2.25%
143. (729 x 15625)1/3 =
(1) 225
(2) 252
(3) 522
(4) 524
1
(729 x 15625)1/3
3√729 x 3√15625
9*25 = 225
144. The roots of equation ax2 + bx + c = O is
(1) [—b ± √(b2 + 4ac)]/2a
(2) [—b ± √(b2 -ac)]/2a
(3) 2c/[—b ± √(b2 - 4ac)]
(4) None of these
3
ax2+bx+c=0
Formula (a+b)(a-b) = a2-b2
Formula for root of x is x=(-b ± √b2 – 4ac)/2a
x=[(-b ± √b2 – 4ac)/2a] * (-b ± √b2 – 4ac)/ (-b ± √b2 – 4ac)
(-b)2 –[√(b2 – 4ac])2 upon 2a[-b ± √(b2 – 4ac)]
b2 - b2 – 4ac upon 2a[-b ± √(b2 – 4ac)]
b2 - b2 =0, 4ac/2a = 2c
2c/[-b ± √(b2 – 4ac)]
145. If the selling price of 320 pens is equal to the cost price of 400 pens, what is the percentage profit ?
(1) 20%
(2) 40%
(3) 25%
(4) 12.5%
3
Selling price of 320 @ x per pen is 320x
Cost of pen = 100, total cost = 400*100 = 40000
Sale value of 320 pen is 40000
Selling price per pen = 40000/320 = 125
Profit 125-100= 25%
146. The sum of the digits of square root of
992016 is
(1) 28
(2) 26
(3) 24
(4) 22
3
√9920016 = 996
9+9+6=24
147. The square root of (0.75)3/0.25 + [1.75 + (0.75)2] is
(1) 1
(2) 2
(3) 3
(4) 4
2
√[(3/4)3/(1/4) + [(7/4) + (3/4)2]
√[(3/4)* (3/4)* (3/4)* (4/1) + (7/4) + (3/4) * (3/4)
√[(27/16)+(7/4) + (9/16)]
√[(27/16)+(37/16) = √64/16
=√4 = 2
148. If √a2+b2= 613, then one of the value of (a + b) is :
(1) 577
(3) 657
(2) 647
(4) 637
2
√a2+b2= 613
√a2+b2= 612+1
Squiring both sides
a2+b2= (612+1)2 identity (a+b)2
a2+b2= 6122+12+2*612*1
a2+b2= 6122+12+1224
a2+b2= 6122+1225
a2+b2= 6122+352
comparing LHS with RHS
a+b = 812+35 =647
149. The sum of the factors of x3+8x2+ 19x+ 12 is
(1) 3x
(2) 3x+4
(3) 3x-8
(4) 3X+8
4
x3+8x2+ 19x+ 12
factors of 12 = 1*2*3*4*6*12 and -2, -3, -4 , -6
if factor of x= -1 then -1+8-19+12= 20-20 = 0 therefore (x+1)is a factor
if factor of x= -2 then -8+32-38+12= -46 therefore (x+2)is not a factor
if factor of x= -3 then -27+13-57+12=84-84= 0 therefore (x+3)is a factor
if factor of x= -4 then -64+18-76+12-140 = 140-140 = 0 therefore (x+4)is a factor
if factor of x= -6 then -1728+1152-228+12=1956 = 0 therefore (x+6)is not a factor
(x+1)+(x+30 +(x+4) = 3x+8
150. If (a/x) + (b/y) =m and (b/x)+ (a/y)= n, then x: y is
(1)(na + mb) : (ma + nb)
(2)(na + mb) : (ma — nb)
(3)(na — mb) : (ma —nb)
(4)(na — mb) : (ma + nb)
3
(a/x)+ (b/y)= m …….(1)
(b/x)+ (a/y)= n ……..(2)
Multiply a with (1) and b with equation (2)
(a2/x)+ (ab/y)= ma
(b2/x)+ (ab/y)= nb
Substracting
(a2/x)- (b2/x) = ma-nb
(a2-b2)/x = ma-nb
x=(a2-b2)/ ma-nb
Similarly Multiply b with (1) and a with equation (2)
(ab/x)+(b2/y)=mb…….(1)
(ba/x)+(a2/y)=na……..(2)
Substracting
(b2/y)-(a2/y) = mb-na
(b2-a2)/y = mb-na
Y=(b2-a2)/ mb-na
x/y = [(a2-b2)/ ma-nb]/[(b2-a2)/ mb-na]
(b2-a2)/na-mb : [(b2-a2)/ mb-na
(na-mb) : (mb-na)
SMART
LEARNING WITH B M GAUR - 9462900411
NEXTGEN
CAREER COACHING-www.facebook.com/nextgencareer
http://facebook.com/groups/nextgencareers